3-1: Introduction

আজকের মডিউল শেষ করলে আমরা যে যে বিষয় গুলা জানতে পারবো

1. Prefix Sum নিয়ে জানতে পারবো
2. Prefix Sum কেনো ব্যবহার করতে হয় তা জানতে পারবো
3. Prefix Sum এর ইমপ্লিমেন্টেশন জানতে পারবো
4. বাইনারি সার্চ সম্পর্কে জানতে পারবো
5. বাইনারি সার্চের কেনো প্রয়োজন তা জানতে পারবো
6. বাইনারি সার্চ এর ইমপ্লিমেন্টেশন জানতে পারবো

Range Sum Query (Codeforces)

Problem Link : https://codeforces.com/group/MWSDmqGsZm/contest/219774/problem/Y

Question Analysis :

প্রবলেমে বলা হয়েছে আপনাকে দুইটি নাম্বার N এবং Q দেয়া হবে।​ ​ একটি N সাইজের এরে দেয়া হবে। এরপর থেকে Q সংখ্যক কুয়েরি জিজ্ঞেস করা হবে যেখানে​ ​ প্রত্যেকটি কুয়েরি তে দুটি ভ্যালু দেয়া থাকবে L এবং R. আপনার প্রত্যেকটি কুয়েরি এর জন্য উত্তর দিতে হবে , উক্ত এরেটি্র​ ​ L নম্বর পজিশন থেকে R নম্বর পজিশন পর্যন্ত যে ভ্যালু গুলা আছে তাদের যোগফল কতো।

Example Analysis :

আমরা দ্বিতীয় Example টি নিয়ে আলোচনা করবো।

এখানে কুয়েরি গুলা হলোঃ প্রথম কুয়েরি -> 1 3 অর্থাৎ L এর মান হলো ১ এবং R এর মান হলো ৩। অর্থাৎ আমাদের ১ নাম্বার পজিশন থেকে ৩ নাম্বার পজিশন পর্যন্ত যে ভ্যালু গুলা আছে তার যোগ ফল দেখাতে হবে । যোগ ফল হলো = ৫+৫+২ = ১২। তাই 1 3 এর জন্য উত্তর এসেছে 12.

দ্বিতীয় কুয়েরি -> 2 3 অর্থাৎ L এর মান হলো ২ এবং R এর মান হলো ৩। অর্থাৎ আমাদের ২ নাম্বার পজিশন থেকে ৩ নাম্বার পজিশন পর্যন্ত যে ভ্যালু গুলা আছে তার যোগ ফল দেখাতে হবে । যোগ ফল হলো = ৫+২ = ৭। তাই 2 3 এর জন্য উত্তর এসেছে 7.

তৃতীয় কুয়েরি -> 1 4 অর্থাৎ L এর মান হলো ১ এবং R এর মান হলো ৪ । অর্থাৎ আমাদের ২ নাম্বার পজিশন থেকে ৩ নাম্বার পজিশন পর্যন্ত যে ভ্যালু গুলা আছে তার যোগ ফল দেখাতে হবে । যোগ ফল হলো = ৫+২ = ৭। তাই 2 3 এর জন্য উত্তর এসেছে 15.

আসেন আমরা প্রবলেমটির সহজ সরল একটি সলিউশন লেখার চেষ্টা করি।

Naive Approach :

#include <bits/stdc++.h>

using namespace std;


int main()

{

int N, Q;
cin >> N >> Q;

vector<int> V(N);

for (int i = 0; i < N; i++) // O(N)
{
cin >> V[i];
}


for (int i = 1; i <= Q; i++) // O(Q)
{

int L, R;
cin >> L >> R;
L--; R--; // converting the position to array index

int SUM = 0;

for (int j = L; j <= R; j++) // O(N) -> কারণ আমাদের প্রত্যেকবার L এর মান ১ এবং R এর মান N পর্যন্ত দেয়া হতে পারে
{

SUM += V[j];
}

cout << SUM << endl;

}

}

Code Explanation :

উক্ত কোডে আমরা ১৭ নাম্বার লাইন থেকে আমাদের মেইন কুয়েরির পার্ট টুকু করেছি ।​ ​ এখানে আমরা দুটি নাম্বার L এবং R​ ​ এর ভ্যালু ইনপুটে নিচ্ছি যা মুলত আমাদের রেঞ্জ। এরপর আরেকটি লুপ চালাচ্ছি এই রেঞ্জের জন্য from L to R এবং এই রেঞ্জের​ ​ মধ্যে যে​ ​ এরে এলিমেন্ট গুলা আছে তা যোগ করছি।​ ​ এবং সবশেষে এই যোগফলটি প্রিন্ট করে দিচ্ছি

এই কোডের টাইম কমপ্লেক্সিটি হলো O (Q*N).

এখন প্রবলেমে আমাদের N এর মান এবং Q এর মান 10^5 পর্যন্ত দেয়া থাকতে পারে .​ ​ যেহেতু আমাদের কোডের টাইম কমপ্লেক্সিটি O(Q*N) , তাই এই ইনপুটের জন্য আমাদের কোডে Total (10^5 * 10^5) = 10^10 টি অপারেশন চলবে। যেহেতু কম্পিউটার এক সেকেন্ডে 10^8 টি অপারেশন করতে পারে,​ ​ তাই এই এপ্রোচে এই প্রবলেমটি সল্ভ করা যাবে না।​ ​ এবং সাবমিট করলে এই প্রবলেমটি TLE দেখাবে।

আমরা সামনে একটি টেকনিক শিখবো যার মাধ্যমে এই প্রবলেমটি খুব সহজে এই টাইম লিমিটের মধ্যে করতে পারবো।

Prefix Sum পরিচিতি

আগের সলিউশন টা নিয়ে চিন্তা করে দেখলে আমরা দেখতে পারি এখানে প্রাইমারি লুপ যেটা দিয়ে আমরা কুয়েরি গুলা উত্তর করছি তা কোন ভাবেই কমানো পসিবল না। এবং এই লুপ টা চালালে আমার given time complexity এর মধ্যে প্রোগ্রামটি রান করবে। এখানে যে লুপটি আসলে প্রবলেম ক্রিয়েট করছে তা হলো কুয়েরি এর ভিতরের লুপ যার দ্বারা আমরা যোগফল বের করতেছিলাম। এই লুপ টা কীভাবে বাদ দেয়া যায় আসেন তা নিয়ে একটু চিন্তা করি।

এই প্রবলেমটি সমাধান করতে হলে আমাদের একটি নতুন টেকনিক সম্পর্কে জানতে হবে। এই টেকনিকের নাম প্রিফিক্স সাম টেকনিক। যার মাধ্যমে আমরা একটি এরে এর একটি নির্দিষ্ট রেঞ্জের যোগ ফল শুধু মাত্র O(1) টাইম কমপ্লেক্সিটি তে বলে দিতে পারবো।

প্রিফিক্স সাম টেকনিক মুলত একটি প্রিফিক্স সামের এরে তৈরি করে যেখানে প্রিফিক্স সামের প্রতিটি ইন্ডেক্স i এ, অরিজিনাল এরে এর 0 থেকে i পর্যন্ত সকল ইন্ডেক্সের ভ্যালু এর যোগফল স্টোর করা থাকবে।

একটি এরে এর উদাহরণের মাধ্যমে দেখার চেষ্টা করি বিষয়টা

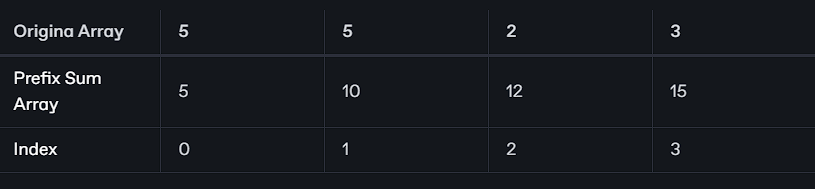
উক্ত এরে এর জন্য কিছু কুয়েরি দিয়ে উত্তর টা বের করার মাধ্যমে প্রিফিক্স সাম টেকনিক কীভাবে কাজ করছে দেখার চেষ্টা করি।

যদি আমাকে জিজ্ঞেস করা হয়

১। অরিজিনাল এরে এর Ar[0] থেকে Ar[3] পর্যন্ত ভ্যালু গুলার যোগফল কতো। তাহলে আমরা প্রিফিক্স সাম এরে এর 3 নাম্বার ইন্ডেক্স এর ভ্যালু বলে দিলে হয়ে যাবে যা হলো ১৫ । কারণ আমরা জানি প্রিফিক্স সামের এরে এর 3rd index এ অরিজিনাল এর ০ থেকে ৩ নাম্বার পর্যন্ত ইন্ডেক্সের যোগফল আছে অর্ Prefix_sum_array[3] = ar[0] + ar[1] + ar[2] +ar[3] .

২। যদি জিজ্ঞেস করা হয় এরে এর 2 নাম্বার ইন্ডেক্স পর্যন্ত ভ্যালু গুলার যোগফল কতো তবে তা আমরা প্রিফিক্স সাম এরে এর ২ নাম্বার ইন্ডেক্স দেখলে পেয়ে যাবো, কারণ Prefix_sum_array[2] = ar[0] + ar[1] + ar[2] =12

৩। যদি জিজ্ঞেস করা হয় এরে এর 1 নাম্বার ইন্ডেক্স পর্যন্ত ভ্যালু গুলার যোগফল কতো তবে তা আমরা প্রিফিক্স সাম এরে এর 1 নাম্বার ইন্ডেক্স দেখলে পেয়ে যাবো, কারPrefix_sum_array[1] = ar[0] + ar[1] = 10

৪। এখন যদি আমাদের বলা হয় , এরে এর প্রথম থেকে নিয়ে কোন একটি নির্দিষ্ট ইনডেক্সের যোগফল নয় বরং একটি নির্দিষ্ট ইন্ডেক্স থেকে অপর একটি নির্দিষ্ট ইনডেক্সের যোগফল যদি চাওয়া হয় , তবে তা কীভাবে করবো । আসুন , একটি উদাহরণের সাহায্যে দেখার চেষ্টা করি।

ধরুন বলা হলো এরে এর 2 নাম্বার ইনডেক্স থেকে 3 নাম্বার ইনডেক্স এর যোগফল কতো ? খেয়াল করলে দেখবেন ,Prefix_sum_array[3] = ar[0] + ar[1] + ar[2] +ar[3] অর্থাৎ প্রিফিক্স সাম এরে এর ইনডেক্স ৩ তে ০ থেকে নিয়ে ৩ নাম্বার ইনডেক্সের সব ভ্যালু যোগ করা আছে। এখন আমরা যদি চাই এরে এর ২ নাম্বার ইনডেক্স থেকে ৩ নাম্বার ইনডেক্সের মান বের করতে তবে আমাদের ar[0] + ar[1] এই অংশটুকু বাদ দিতে হবে।

আবার , Prefix_sum_array[1] = ar[0] + ar[1] এ স্টোর আছে ।

তার মানে ২ থেকে ৩ নাম্বার ইন্ডেক্সের যোগফল

= Prefix_sum_array[3] - Prefix_sum_array[1]

= ar[0] + ar[1] + ar[2] +ar[3] - ar[0] + ar[1] = ar[2] +ar[3] যা আমাদের ২ এবং ৩ নাম্বার ইনডেক্সের ভ্যালুর যোগফল ।

আমাদের যদি জিজ্ঞেস করা হয় কোন একটি এরে এর L তম ইনডেক্স থেকে R তম ইন্ডেক্সের ভ্যালু গুলার যোগফল কতো , তবে আমরা খুব সহজে প্রিফিক্স সাম এর এরে থেকে তা বলে দিতে পারবো , তা হলো

Sum (L,R) = Prefix_sum_array[R] - Prefix_sum_array[L-1]

Prefix sum ইমপ্লিমেন্টেশন

মুলত আমাদের প্রধান উদ্দেশ্য হলো মেইন এরে থেকে Prefix Sum এর এরে টি তৈরি করা। এবং আগের Range sum Query er প্রবলেমটি সল্ভ করবো।

Code of Range Sum Query using Prefix Sum Technique :

#include <bits/stdc++.h>

using namespace std;


int main()

{

int N, Q;
 cin >> N >> Q;

vector<long long int> V(N);

for (int i = 0; i < N; i++) // O(N)
{
 cin >> V[i];
}


vector<long long int> prefix_sum(N);

 prefix_sum[0] = V[0] ; // প্রিফিক্স সাম এরে এর প্রথম ভ্যালুটি হবে এরে এর প্রথম ভ্যালুটি

 for(int i =1 ;i<N ;i++){
 prefix_sum[i] = prefix_sum[i-1]+V[i] ;
 }

 for (int i = 1; i <= Q; i++) // O(Q)
 {

int L, R;
 cin >> L >> R;
 L--; R--; // converting the position to array index

long long int SUM = 0;

 // for (int j = L; j <= R; j++) // O(N) -> কারণ আমাদের প্রত্যেকবার L এর মান ১ এবং R এর মান N পর্যন্ত দেয়া হতে পারে
 // {

 // SUM += V[j];
 // } // এই লুপটি বাদ দিয়ে এখন আমরা প্রিফিক্স সাম টেকনিক ব্যবহার করবো


 if(L==0){
 SUM = prefix_sum[R];
 } // যদি L এর মান ০ হয় তবে L-1 invalid হয়ে যাবে। সেইক্ষেত্রে শুরু থেকে নিয়ে R পর্যন্ত হবে সাম
 else SUM = prefix_sum[R]-prefix_sum[L-1] ; // O(1)

 cout << SUM << endl;
 }

}

প্রিফিক্স সাম এরে টি তৈরি করার প্রক্রিয়াঃ

1. যেহেতু আমরা জানি , যেখানে প্রিফিক্স সামের প্রতিটি ইন্ডেক্স i এ, অরিজিনাল এরে এর 0 থেকে i পর্যন্ত সকল ইন্ডেক্সের ভ্যালু এর যোগফল স্টোর করা থাকবে তাই prefix_sum[0] = V[0] সেট করে দেয়া হয়েছে কারণ প্রিফিক্স সাম এরে এর ০ তম ইন্ডেক্সে শুধু মাত্র মেইন এরে এর ০ তম ইন্ডেক্স এর ভ্যালু থাকবে ।
2. এরপর prefix_sum[1] এ থাকবে V[0] + V[1]। যেহেতু prefix_sum[0] = V[0] তাই আমরা prefix_sum[1] এ prefix_sum[0] + V[1] করলাম
3. এরপর prefix_sum[2] এ থাকবে V[0] + V[1] +V[2]. যেহেতু prefix_sum[1] = V[0] +V[1] তাই আমরা prefix_sum[2] এ prefix_sum[1] + V[2] করলাম.
4. এইভাবে করে আমরা n-1 পর্যন্ত সব ভ্যালু গুলা O(N) টাইমে বের করে ফেলতে পারবো।

এইবার আমরা Sum (L,R) = Prefix_sum[R] - Prefix_sum[L-1]​ ​ এই সুত্রের সাহায্যে প্রতিটি কুয়েরি এর উত্তর O(1) এ দিতে পারবো ।

এখন যদি আমরা পুরো কোড টির টাইম কমপ্লেক্সিটি এনালাইসিস করি তবে দেখতে পারবো , এর টাইম কমপ্লেক্সিটি হলো O(N + Q1) এবং N , Q <= 10^5 তাই এই কোডের total operations হবে 10^5+10^5 = 2 10^5 . যা এক সেকেন্ডের মধ্যে খুব সহজে পাস করে ফেলবে। সুতারাং আমরা আমাদের আগের O(Q*N) / O (N^2) কমপ্লেক্সিটি থেকে এখন O(N) এ নিয়ে আসলাম কমপ্লেক্সিটি যা আসলে অনেক বিরাট ইম্প্রুভমেন্ট। এর থেকে বুঝা যায় প্রিফিক্স সাম টেকনিক এর গুরুত্ব আসলে কতটুকু।

Binary Search (Codeforces)

Problem Link : https://codeforces.com/group/MWSDmqGsZm/contest/219774/problem/Z

Question Analysis :

প্রবলেমে বলা হয়েছে আপনাকে দুইটি নাম্বার N এবং Q দেয়া হবে। একটি N সাইজের এরে দেয়া হবে। এরপর থেকে Q সংখ্যক কুয়েরি জিজ্ঞেস করা হবে যেখানে প্রত্যেকটি কুয়েরি তে একটি ভ্যালু দেয়া থাকবে X . আপনার প্রত্যেকটি কুয়েরি এর জন্য উত্তর দিতে হবে , উক্ত এরেটি্র মধ্যে X ভ্যালুটি আছে কিনা ।

Example Analysis : আমরা Example টি নিয়ে আলোচনা করবো।

এখানে কুয়েরি গুলা হলোঃ প্রথম কুয়েরি -> X = 5 , অর্থাৎ 5 এই এরে এর মধ্যে আছে কিনা তা উত্তর দিতে বলা হয়েছে। এই এরে এর 1 নাম্বার ইনডেক্স এ ভ্যালু 5 আছে। তাই এর উত্তর হলো found.

দ্বিতীয় কুয়েরি -> X = 3 , অর্থাৎ 3 ভ্যালুটি এই এরে এর মধ্যে আছে কিনা তা উত্তর দিতে বলা হয়েছে। এই এরে এর 3 নাম্বার ইনডেক্স এ ভ্যালু 3 আছে। তাই এর উত্তর হলো found.

তৃতীয় কুয়েরি -> X = 6 , অর্থাৎ 6 ভ্যালুটি এই এরে এর মধ্যে আছে কিনা তা উত্তর দিতে বলা হয়েছে। এই এরে এর কোন ইন্ডেক্সে ভ্যালু 6 নেই। তাই এর উত্তর হলো not found.

Naive approach :

#include <bits/stdc++.h>

using namespace std;


int main()

{

int N, Q;
 cin >> N >> Q;

int array[N];

for (int i = 0; i < N; i++)
{
 cin >> array[i];
}

for (int i = 0; i < Q; i++) // O (Q)
{

int X;
 cin >> X;

int flag = 0;

for (int j = 0; j < N; j++) // O (N)
{

if (array[j] == X)
{

flag = 1;
}
}

if (flag)
 cout << "found" << endl;
 else
 cout << "not found" << endl;
 } // O (Q*N)

}

আমরা প্রতিটি কুয়েরি এর জন্য একটি লুপ চালাচ্ছি যার কমপ্লেক্সিটি হবে O (Q) এবং কোন ভ্যালু টা খুজতে হবে তা ইনপুট এ নিচ্ছি । এরপর ঐ লুপের এরে টির প্রত্যেকটি এলিমেন্টে লুপের সাহায্যে যেয়ে দেখবো যে আমাদের টার্গেট ভ্যালু এর সাথে মিলছে কিনা। এবং এরের সাইজ যেহেতু N তাই আমাদের প্রত্যেকটি কুয়েরি তে worst case এ পুরো এরেটি খুজে দেখতে হবে , তাই ভিতরের লুপের কমপ্লেক্সিটি O(N) , তাই এই কোডের overall টাইম কমপ্লেক্সিটি হলো O(Q*N).

এখন প্রবলেমের constraints এ N এবং Q এর মান ম্যাক্সিমাম 10^5 পর্যন্ত হতে পারে। সুতারাং worst case এ আমাদের O(Q*N) কমপ্লেক্সিটি এর কোড (10^5 * 10^5) টি = 10^10 অপারেশন করবে। এবং যেহেতু আমরা জানি 1sec e ম্যাক্সিমাম 10^8 টি অপারেশন করা যায় , তাই এই কোড এক সেকেন্ড এ পাস করবে না এবং TIME LIMIT EXCEEDED হবে।

সুতারাং আমাদের এই কোড টি আরও অপটিমাইজ করতে হবে। নেক্সট পেইজে আমরা এই বিষয় সম্পর্কে জানবো।

বাইনারি সার্চ পরিচিতি

বাইনারি সার্চে একটি অনেক অপ্টিমাইজড সার্চ এলগরিদম যার সাহায্যে আমরা একটি এরেতে একটি ভ্যালু খুব ভালো মানের একটি টাইম কমপ্লেক্সিটি এর সাহায্যে খুঁজতে পারি। আসেন একটি উদাহরণের সাহায্যে বিষয়টি দেখার চেষ্টা করি।

মনে করেন আপনাকে একটি এরে দেওয়া হল যেখানে নিজের ভ্যালু গুলা আছে

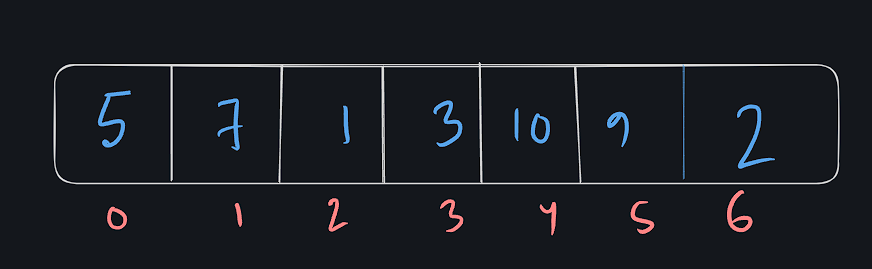
এবং আপনাকে বলা হলো এই এরেতে ভ্যালু ৭ আছে কিনা খুজে দেখতে বলা হয়েছে । এরেটি কে আমরা ছোট থেকে বড় আকারে সাজালে এখানে একটি সুন্দর টেকনিক সম্পর্কে আমরা জানতে পারবো , আসেন এরে টি কে সর্ট করে নেয়।

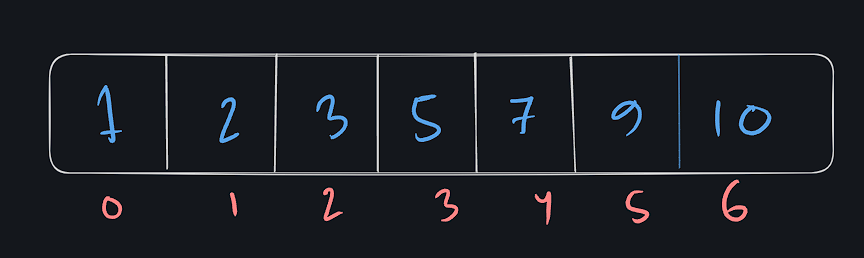
এখন আমরা একটা কাজ করতে পারি , আমাদের যেহেতু 7 আছে কিনা দেখতে বলা হয়েছে , আমরা এরে এর ঠিক মাঝখানের ভ্যালু টি নিয়ে চেক করে দেখবো এটি 7 কিনা। মাঝের ভ্যালুটি থাকবে = (0+6) /2 = 3 নাম্বার ইন্ডেক্সে।

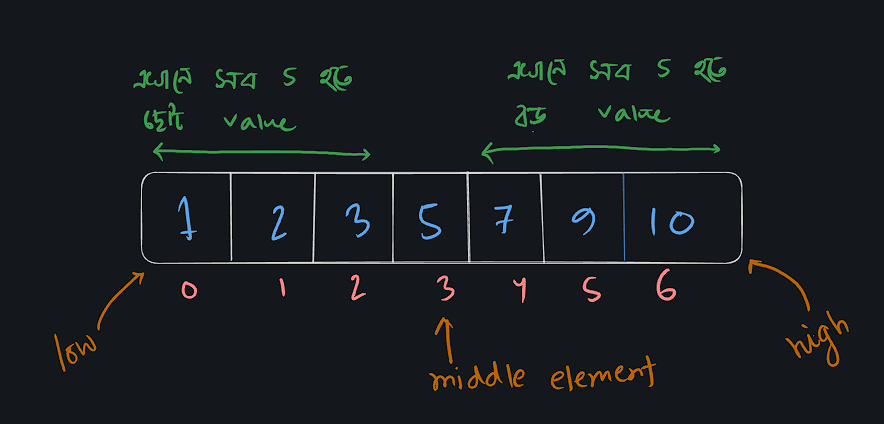
এখানে মাঝখানের ভ্যালুটি হলো ৫ যা 7 এর সমান নয়।

এখন আসেন আমরা এরে থেকে কিছু প্রশ্ন করি

1. প্রথম প্রশ্ন , আমরা যেহেতু মাঝখানে ভ্যালু ৫ পেয়েছি যা আমাদের কাঙ্খিত ভ্যালু ৭ এর থেকে কম। এখন কি মনে হয় মধ্যখানের বাম পাশে যে ভ্যালু গুলা আছে তার মধ্যে ৭ কে খুজে পাওয়ার কোনো সম্ভাবনা আছে কি ? -> যেহেতু আমরা যে ভ্যালু খুজছি ৭ তা ৫ থেকে বড় এবং ৫ এর বাম পাশে যে ভ্যালু গুলা আছে তা সব ৫ থেকেই ছোট তাই এরেটির ৫ এর বাম পাশের অংশটুকু তে কখনো ৭ ভ্যালুটি পাওয়া সম্ভব না।
2. দ্বিতীয় প্রশ্ন , যদি আমরা এতটুকু নিশ্চিত থাকি যে , এরে এর মধ্যখানে ভ্যালু ৫ এর বাম পাশে সব ৫ হতে ছোট ভ্যালু এবং সেখানে ৭ ভ্যালুটি খুজে পাওয়া কখনো সম্ভব না, আমাদের ৯ ভ্যালুটি খোজার জন্য আবার এরে এর প্রথম থেকে পুরো ভ্যালুটি খুজতে হবে ? -> উত্তর হলো না, আমরা যেহেতু নিশ্চিত যে এরে এর মধ্যখানের ভ্যালুটি ৫ এবং এর বাম পাশে সব ৫ থেকে ছোট ভ্যালু তাই আমরা তার বাম পাশে আর ৭ খুজবো না। আমরা ৫ এর ডান পাশের অংশটি তে ৭ পাওয়া যায় কিনা খুজে দেখবো। অর্থাৎ আমরা আমাদের এরে এর searching space টি কে এখন অর্ধেক করে ফেললাম।

আমরা এখন এরেটির নিচের এই অংশের মধ্যে ভ্যালু ৭ খুজবো

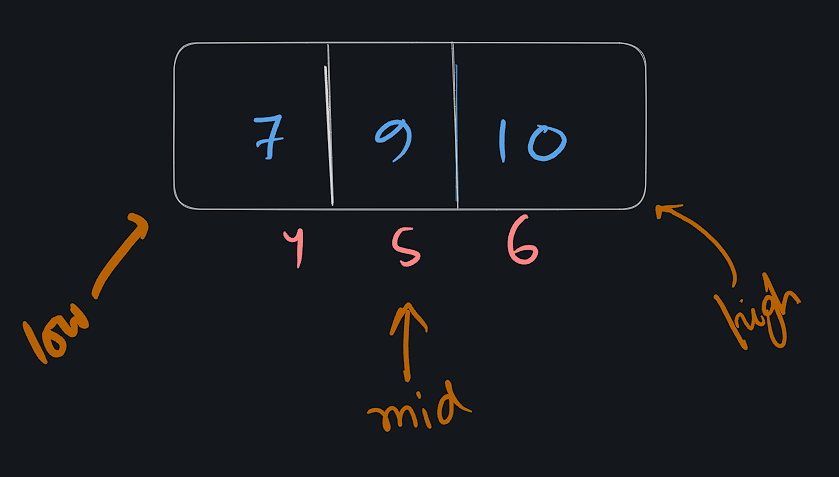
এরপর আমরা আবার একই ভাবে মধ্যখানের ভ্যালুটি চেক করে দেখবো । মধ্য খানের ভ্যালু টি থাকবে (4+6) /2= 10/2 = 5 নাম্বার ইন্ডেক্সে। এখন চেক করে দেখবো এরেটির 5 নাম্বার ইনডেক্সে ভ্যালু ৭ আছে কিনা। এরেটির 5 নাম্বার ইনডেক্সে ৯ ভ্যালুটি আছে। আবার আগের মতো চিন্তা করে দেখি ,

1. আমাদের এরেটি ছোট থেকে বড় আকারে সাজানো হয়েছে এবং আমরা আমাদের searching space এর মধ্য খানে পেয়েছি ৯ , অর্থাৎ ৯ এর বাম পাশের সব ভ্যালু হবে ৯ হতে ছোট এবং ডান পাশের সব ভ্যালু গুলা হবে ৯ এর থেকে বড়
2. যেহেতু আমরা ভ্যালু ৭ কে খুজছি এবং ৭, ৯ হতে ছোট । সুতারাং এটি আমরা নিশ্চিত যে , ৯ এর ডান পাশে কখনো ভ্যালু ৭ পাওয়া সম্ভব না। আমরা ৯ এর বাম পাশে ভ্যালু ৭ খুজবো। অর্থাৎ আমরা আবারো আমাদের searching স্পেস কে অর্ধেক করে ফেললাম।

আমরা এখন এরেটির নিচের এই অংশের মধ্যে ভ্যালু ৭ খুজবো

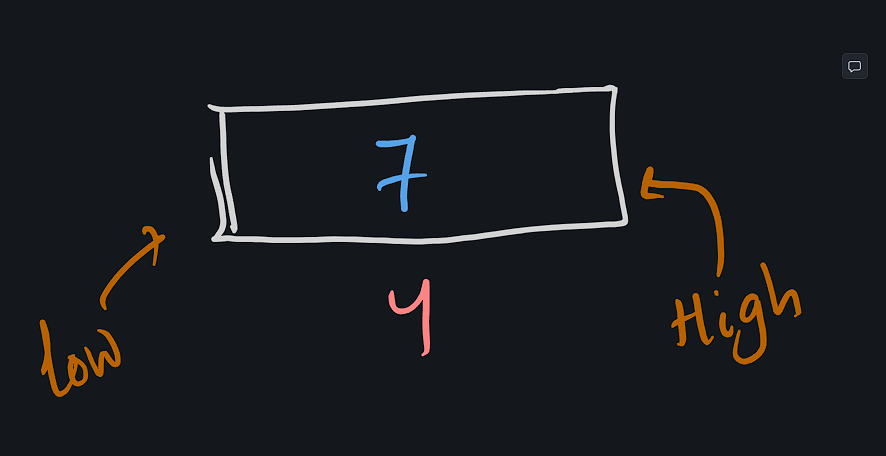
এখন এরের এই অংশটুকুর মধ্য হচ্ছে (4+4)/2 = 8/2 = 4 নাম্বার ইন্ডেক্স। যা আমাদের কাঙ্খিত ভ্যালু 7 এর সমান।

টাইম কমপ্লেক্সিটি :

এখানে যেহেতু আমরা আমাদের প্রত্যেকটি স্টেপ পর পর এরে টির অর্ধেক অংশ কে বাদ দিয়ে দিচ্ছি এবং আমরা জানি যে , যদি এমন হয় প্রত্যেকটা স্টেপ পর পর যদি আমাদের কোন একটা ভ্যরিয়েবল এর মান অর্ধেক হারে কমতে থাকে তবে ঐ কোডের টাইম কমপ্লেক্সিটি হবে O(logn)। বাইনারি সার্চের ক্ষেত্রে আমাদের এরে এর যে অংশ টুকু তে মানটি খুজছি অর্থাৎ আমাদের searching space প্রতিটি স্টেপ এ অর্ধেক হয়ে যাচ্ছে।

বাইনারি সার্চের টাইম কমপ্লেক্সিটি হলো O (logN )​ ​

বাইনারি সার্চ ইমপ্লিমেন্টেশন

আমরা গত সেকশনে বাইনারি সার্চ কীভাবে কাজ করে তা জানলাম। এখন আমরা শিখবো কীভাবে আমরা তা কোডে ইমপ্লিমেন্ট করতে পারি ।

বাইনারি সার্চ ইমপ্লিমেন্ট করতে হলে array টি অবশ্যই ascending order এ sorted থাকতে হবে।

বাইনারি সার্চ ইমপ্লিমেন্ট করার ক্ষেত্রে আমাদের কিছু স্টেপ ফলো করতে হবে।

1. প্রথমে আমাদের নির্ধারণ করতে হবে আমরা এই স্টেপে এরে কত টুকু অংশ জুড়ে এই ভ্যালুটি খুজবো , যাকে আমরা বলতেছি searching space. শুরুতে পুরো এরেটি আমাদের searching space হবে। আমরা দুটি ভ্যারিয়েবল low এবং high রাখবো যার সাহায্যে এই স্টেপে এরে এর কতটুকু অংশ নিয়ে কাজ করবো তার ট্র্যাক রাখবো। শুরুতে যেহেতু আমরা পুরো এরেতেই ভ্যালুটি খুজছি , তাই low পয়েন্ট করবে এরে এর o তম ইন্ডেক্সে এবং high পয়েন্ট করবে এরে এর শেষ ইনডেক্স n-1 এ। অর্থাৎ low = 0 , high = n-1
2. এরপর আমরা searching space এর mid বের করবো । mid index হবে​ ​ (low+high)/2
3. এরপর চেক করে দেখবো mid index এ যে ভ্যালু আছে তা আমাদের কাঙ্খিত target এর সমান কিনা। সমান হলে এখানে​ ​ সার্চ করা বন্ধ করে দিবো।
4. যদি আমাদের কাঙ্খিত ভ্যালু থেকে mid index এর ভ্যালু বড় হয় , তাহলে আমরা নিশ্চিত যে , ঐ মিড এলিমেন্ট ডান অংশে কখনো কাঙ্খিত ভ্যালু টি থাকতে পারে না , শুধু মাত্র mid এলিমেন্ট এর বাম অংশে থাকতে পারে। তাই আমরা আমাদের searching space টা mid index er বাম সাইডে নিয়ে আসবো । অর্থাৎ ,high = mid -1 করে দিবো।
5. যদি আমাদের কাঙ্খিত ভ্যালু থেকে mid index এর ভ্যালু ছোট হয় , তাহলে আমরা নিশ্চিত যে , ঐ মিড এলিমেন্ট বাম অংশে কখনো কাঙ্খিত ভ্যালু টি থাকতে পারে না , শুধু মাত্র mid এলিমেন্ট এর ডান অংশে থাকতে পারে। তাই আমরা আমাদের searching space টা mid index er ডান সাইডে নিয়ে আসবো । অর্থাৎ ,low = mid +1 করে দিবো।
6. এই স্টেপ গুলা আমরা করতে থাকবো যতক্ষন আমাদের একটা valid searching space থাকবে। অর্থাৎ যতক্ষন low<=high হবে ।

Code implementation :

#include <bits/stdc++.h>

using namespace std;


int main()

{

int N, Q;
 cin >> N >> Q;

int array[N];

for (int i = 0; i < N; i++) // O(N)
{
 cin >> array[i];
}

sort(array, array + N); // O(NlogN) এরে সর্ট করা হলো , যেহেতু বাইনারি সার্চের পূর্বশর্ত হলো এরে সর্ট থাকা

for (int i = 0; i < Q; i++) // O(Q)
{

int X;
 cin >> X;

int flag = 0;

// Binary Search O (logN)

int low = 0, high = N - 1; // low এবং high ভ্যারিয়েবলের মাধ্যমে আমরা searching space নির্ধারণ করলাম

while (low <= high) // যতক্ষন এরেতে সার্চ করার মতো atleast একটি ভ্যালু থাকে।
{
int mid_index = (low + high) / 2; // mid index বের করছি

if (array[mid_index] == X) // যদি searching space এর মধ্যখানের element এর মান কাঙ্খিত মানের সমান হয়
{
 flag = 1; // তবে flag এর মান ১ করে সার্চ করা এখানে বন্ধ করে দিচ্ছি
 break;
}
else if (array[mid_index] > X) // যদি searching space এর মধ্যখানের element এর মান কাঙ্খিত মানের চেয়ে বড় হয়
{
 high = mid_index - 1; // তবে আমরা mid_index এর ডান সাইডের অংশ টুকু বাদ দিচ্ছি ,অর্থাৎ high কে mid_index এর ডানে নিয়ে আসছি
}
else if (array[mid_index] < X) // যদি searching space এর মধ্যখানের element এর মান কাঙ্খিত মানের চেয়ে ছোট হয়
{
 low = mid_index + 1; // তবে আমরা mid_index এর বাম সাইডের অংশ টুকু বাদ দিচ্ছি ,অর্থাৎ low কে mid_index এর ডানে নিয়ে আসছি
}
}

if (flag)
 cout << "found" << endl;
 else
 cout << "not found" << endl;
 }

}

Time complexity Analysis :

উক্ত কোডের টাইম কমপ্লেক্সিটি হবে O (N + NlogN + QlogN) => O (QlogN). এখন প্রবলেমের constraints এ N এবং Q এর মান ম্যাক্সিমাম 10^5 পর্যন্ত হতে পারে। সুতারাং worst case এ আমাদের কোডটি O(Q*logN) অর্থাৎ (10^5 * log2(10^5)) = (10^5 * 17) = 17 *10^5 টি অপারেশন করবে। এবং যেহেতু আমরা জানি 1sec e ম্যাক্সিমাম 10^8 টি অপারেশন করা যায় , তাই এই কোড এক সেকেন্ড এ খুব সহজে পাস করবে।

খুব চমৎকার একটি বিষয়। আমরা আমাদের কোডের কমপ্লেক্সিটি O( QN) হতে কমিয়ে O(QlogN) এ নিয়ে আসলাম যা আসলে অনেক বড় একটি ইম্প্রুভমেন্ট। তাহলে আমরা এই মডিউল শেষে শিখলাম কীভাবে একটি এরে হতে খুব দ্রুত একটি ভ্যালু খুজে বের করে নিয়ে আসতে হয়। আমরা পরবর্তীতে এমন আরো কিছু ইন্টারেস্টিং টেকনিক / এলগরিদম দেখবো। শুভ কামনা রইলো সবার জন্য।