মডিউল ১৮ঃ 2D এরে

মডিউল ১৮-০ঃ সূচনা

এই মডিউলে আমরা কি কি শিখবোঃ

1. 2ডি এরে সম্পর্কে জানবো
2. 2ডি এরে ইনপুট, আউটপুট সম্পর্কে জানবো
3. ম্যাট্রিক্স এবং ম্যাট্রিক্স এর কিছু টাইপ সম্পর্কে জানবো

---

মডিউল 18-1 + 18-2 + 18-3: 2D array কি

আমরা এরে শিখেছি, এরে নিয়ে অনেক কাজও করে ফেলেছি। এতদিন আমরা যেই এরে নিয়ে কাজ করেছি তা ছিল 1D এরে। এবার দেখব 2D এরে।

আমরা দেখেছিলাম, যখন আমাদের অনেকগুলো ভেরিয়েবল লাগতো তখন আমরা অনেকগুলো ভেরিয়েবল না ডিক্লেয়ার করে একটি এরে ডিক্লেয়ার করে কাজ করতাম। এখন যদি আমাদের কখনো একসাথে অনেকগুলো এরের প্রয়োজন হয় তখন আমরা কি করব? একসাথে অনেকগুলো এরে ডিক্লেয়ার করব?

অবশ্যই না। তখন আমরা একটি এরে অফ এরে নিয়ে নিব। অর্থাৎ এমন একটি এরে ডিক্লেয়ার করব যার প্রতিটি ইন্ডেক্সে ভেলু না থেকে থাকবে একটি করে এরে। তাহলে আমরা একটি এরে ডিক্লেয়ার করে অনেকগুলো এরে পেয়ে যাব।

উদাহরন হিসেবে মনে করি একটি ক্লাসে ১০০ জন স্টুডেন্ট আছে। সেই ক্লাসে মোট সাবজেক্ট ১০টি। তাহলে আমি যদি প্রতিটি স্টুডেন্ট প্রতিটি সাবজেক্টে কত পেয়েছে তা আলাদা করে স্টোর করে রাখতে চাই, তাহলে আমাকে ১০০ জন স্টুডেন্ট এর জন্য ১০০টি এরে দরকার। প্রতিটি এরে হবে ১০ সাইজের, যার মধ্যে থাকবে সেই স্টুডেন্ট এর ১০টি সাবজেক্টের মার্ক্স। এক্ষেত্রে আমরা নিশ্চয়ই ১০০টি আলাদা আলাদা এরে ডিক্লেয়ার করব না। আমরা যেটি করব তা হলো একটি 2D ( 2 dimensional ) এরে নিব ১০০ সাইজের। যার প্রতিটি ইন্ডেক্সে থাকবে একটি করে ১০ সাইজের এরে। তাহলে আমরা এই এরেতে প্রথম ইন্ডেক্সে গেলে পাব একটি ১০ সাইজের এরে, তাতে আমরা প্রথম স্টুডেন্ট এর ১০টি সাবজেক্টের মার্ক্স রেখে দিতে পারি। তারপর দ্বিতীয় ইন্ডেক্সে গেলে পাব আরেকটি ১০ সাইজের এরে, তাতে আমরা দ্বিতীয় স্টুডেন্ট এর ১০টি সাবজেক্টের মার্ক্স রেখে দিতে পারি।

এক্ষেত্রে 2D এরে টি আমরা এভাবে ডিক্লেয়ার করতে পারি: int arr [100] [10];

1D এরের মতোই ডিক্লেয়ার করার শুরুতে ডাটা টাইপ বলে দিতে হয়, তারপর এরের নাম, তারপর শুরুতে বলতে হয় কয়টি এরে লাগবে এবং তারপর বলতে হয় প্রতিটি ইন্ডেক্সের মধ্যে যেই এরে লাগবে তার সাইজ।

2D এরে এভাবে কাজ করে। 2D এরের গানিতিক রূপ হচ্ছে ম্যাট্রিক্স।

2D এরের মতোই আমরা চাইলে 3D, 4D, 5D... এরে ডিক্লেয়ার করে নিতে পারি আমাদের প্রয়োজন অনুসারে।

---

মডিউল ১৮-৪ + ১৮-৫ঃ 2D এরে ইনপুট আউটপুট

এবার আমরা দেখব কিভাবে 2D এরে তে ইনপুট নিতে হয় এবং আউটপুট দেখাতে হয়।

1D এরে তে আমরা এরে সাইজ পর্যন্ত একটি লুপ চালিয়ে ইনপুট এবং আউটপুট দেখাতাম। 2D এরেতে আমাদের দুটি নেস্টেড লুপ চালাতে হবে। প্রথম লুপটি ( আউটার লুপ ) 2D এরের সাইজ পর্যন্ত চালাতে হবে এবং দ্বিতীয় ( ইনার লুপ ) লুপটি 2D এরের প্রতিটি ইন্ডেক্সে যেয়ে যেই এরেটি থাকবে তার সাইজ পর্যন্ত চালাতে হবে।

ইনপুট নেওয়ার আগে আমাদের 2D এরের ইন্ডেক্স গুলো কিভাবে হয় তা বুঝতে হবে। 2D এরেতে প্রতিটি ইন্ডেক্সের দুটি করে ভেলু থাকে রো এবং কলাম। আমরা যদি ৫ সাইজের একটি 2D এরে ডিক্লেয়ার করি যার প্রতিটি ইন্ডেক্সে থাকবে একটি করে ৩ সাইজের এরে। তাহলে এরের ইন্ডেক্স গুলো দেখতে হবে এমনঃ

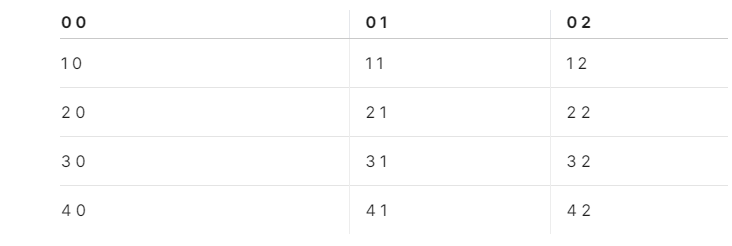
আমরা একটি নেস্টেড লুপ চালিয়ে এরের ইন্ডেক্স গুলো এক্সেস করতে পারিঃ

Code:

#include <stdio.h>
int main()
{
    int a[5][3];                    // 2D এরে ডিক্লেয়ার করা হচ্ছে
    for(int i=0; i<5; i++)          // 2D এরের সাইজ ৫ পর্যন্ত লুপ চালানো হচ্ছে। এই লুপ 2D এরের প্রতিটি ইন্ডেক্সে যাবে।
    {
        for(int j=0; j<3; j++)      // 2D এরের প্রতিটি ইন্ডেক্সে একটি এরে আছে যা ৩ সাইজের, তাই ৩ পর্যন্ত লুপ চালানো হচ্ছে।
        {
            printf("a[%d][%d] ", i, j); // i,j প্রিন্ট করা হচ্ছে, যা 2D এরের রো এবং কলাম প্রিন্ট করবে অর্থাৎ ইন্ডেক্স প্রিন্ট করবে।
        }
        printf("\n");               // ভিতরের এরের সবগুলো ইন্ডেক্স প্রিন্ট করার পর নতুন লাইন প্রিন্ট করা হচ্ছে।
    }
    return 0;
}

কোডটি রান করলে আমরা দেখতে পাব সবগুলো ইন্ডেক্স প্রিন্ট হচ্ছে।

এবার সেইম লজিকে এই ইন্ডেক্সগুলো আমরা scanf() এর মধ্যে দিয়ে ইনপুট নিয়ে নিতে পারি এবং printf() এর মধ্যে দিয়ে আউটপুট দেখিয়ে দিতে পারি।

Code:

#include <stdio.h>
int main()
{
    int a[5][3];                    // 2D এরে ডিক্লেয়ার করা হচ্ছে
    for(int i=0; i<5; i++)
    {
        for(int j=0; j<3; j++)
        {
            scanf("%d", &a[i][j]);   // ইনপুট নেওয়া হচ্ছে।
        }
    }
    for(int i=0; i<5; i++)
    {
        for(int j=0; j<3; j++)
        {
            printf("%d ", a[i][j]);  // আউটপুট প্রিন্ট করা হচ্ছে।
        }
        printf("\n");
    }
    return 0;
}

কোডটি রান করে আমরা ৫টি ৩ সাইজের এরে ( ৫x৩ ম্যাট্রিক্স ) ইনপুট দিলে আউটপুট দেখতে পাব।

---

মডিউল ১৮-৬ + ১৮-৭ঃ 2D এরে প্রিন্টিং বাই রো এন্ড কলাম

এবার আমরা একটি 2D এরে থেকে এক্সাক্ট রো এবং কলাম প্রিন্ট করা দেখব।

শুরুতে আমরা রো এবং কলাম ইনপুট নিয়ে তারপর সেই রো এবং কলাম দিয়ে 2D এরে ডিক্লেয়ার করা দেখে নেই।

Code:

#include <stdio.h>
int main()
{
    int row, col;
    scanf("%d %d", &row, &col);        // রো এবং কলাম সংখ্যা ইনপুট নেওয়া হচ্ছে।
    int a[row][col];                    // ইনপুট নেওয়া রো এবং কলাম দিয়ে 2D এরে ডিক্লেয়ার করা হচ্ছে।
    for(int i=0; i<row; i++)
    {
        for(int j=0; j<col; j++)
        {
            scanf("%d", &a[i][j]);      // নেস্টেড লুপ চালিয়ে ইনপুট নেওয়া হচ্ছে।
        }
    }
    return 0;
}

2D এরেতে আমরা যদি কোন স্পেসিফিক রো প্রিন্ট করতে চাই তাহলে কলাম এর উপর লুপ চালাতে হয় এবং কোন স্পেসিফিক কলাম প্রিন্ট করতে চাই তাহলে রো এর উপর লুপ চালাতে হয়।

Code:

#include <stdio.h>
int main()
{
    int row, col;
    scanf("%d %d", &row, &col);
    int a[row][col];
    for(int i=0; i<row; i++)
    {
        for(int j=0; j<col; j++)
        {
            scanf("%d", &a[i][j]);      // 2D এরে ইনপুট নেওয়া হচ্ছে।
        }
    }
    int r;
    scanf("%d", &r);                    // যেই রো প্রিন্ট করতে চাই তা ইনপুট নেওয়া হচ্ছে।
    for(int i=0; i<col; i++)            // কলামের উপর লুপ চালানো হচ্ছে।
    {
        printf("%d ", a[r][i]);        // ইনপুট নেওয়া রো নাম্বার ফিক্সড রেখে কলামের মধ্যে লুপের ভেরিয়েবলটি দিয়ে দেওয়া হচ্ছে।
    }
    int c;
    scanf("%d", &c);                    // যেই কলাম প্রিন্ট করতে চাই তা ইনপুট নেওয়া হচ্ছে।
    for(int i=0; i<row; i++)            // রো এর উপর লুপ চালানো হচ্ছে।
    {
        printf("%d ", a[i][c]);        // ইনপুট নেওয়া কলাম নাম্বার ফিক্সড রেখে রো এর মধ্যে লুপের ভেরিয়েবলটি দিয়ে দেওয়া হচ্ছে।
    }
    return 0;
}

কোডটি রান করে একটি 2D এরে ইনপুট দিয়ে তারপর একটি রো নাম্বার ইনপুট দিলে সেই এক্সাক্ট রো প্রিন্ট হবে। তারপর একটি কলাম নাম্বার ইনপুট দিলে সেই এক্সাক্ট কলাম প্রিন্ট হবে।

---

মডিউল ১৮-৮ঃ ম্যাট্রিক্স এর প্রকারভেদ

2D এরের গানিতিক রূপ হচ্ছে ম্যাট্রিক্স। এখন আমরা বিভিন্ন ধরনের ম্যাট্রিক্স দেখব।

ম্যাট্রিক্স এ কিছু রো এবং কলাম থাকে। ম্যাট্রিক্স এর ডাইমেনশন রো এবং কলাম দ্বারা প্রকাশ করা হয়। একটি ম্যাট্রিক্স এ যদি ৩টি রো এবং ৫টি কলাম থাকে তাহলে তাকে ( ৩ x ৫ ) ম্যাট্রিক্স বলা হয়।

বিভিন্ন ধরনের ম্যাট্রিক্সঃ

রো ম্যাট্রিক্সঃ

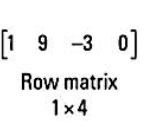
রো ম্যাট্রিক্স হলো এমন ম্যাট্রিক্স যাতে শুধুমাত্র একটি রো থাকে। পাশের ম্যাট্রিক্সটিতে ১টি রো এবং ৪টি কলাম রয়েছে। তাই এটি একটি ১ x ৪ রো ম্যাট্রিক্স।

কলাম ম্যাট্রিক্সঃ

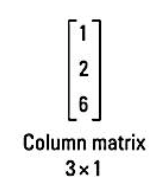
কলাম ম্যাট্রিক্স হলো এমন ম্যাট্রিক্স যাতে শুধুমাত্র একটি কলাম থাকে। পাশের ম্যাট্রিক্সটিতে ৩টি রো এবং ১টি কলাম রয়েছে। তাই এটি একটি ৩ x ১ কলাম ম্যাট্রিক্স।

জিরো বা নাল ম্যাট্রিক্সঃ

জিরো ম্যাট্রিক্স হলো এমন ম্যাট্রিক্স যার সবগুলো ভেলুই জিরো থাকে। পাশের ম্যাট্রিক্সটিতে ৩টি রো এবং ৫টি কলাম রয়েছে, যার সবগুলো ভেলুই জিরো। তাই এটি একটি ৩ x ৫ জিরো বা নাল ম্যাট্রিক্স।

স্কয়ার ম্যাট্রিক্সঃ

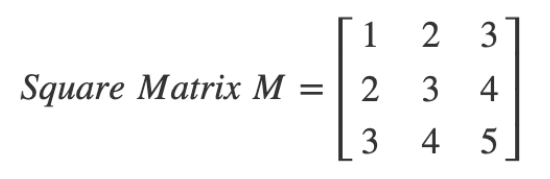
স্কয়ার ম্যাট্রিক্স হলো এমন ম্যাট্রিক্স যার রো এবং কলাম সংখ্যা সমান থাকে। পাশের ম্যাট্রিক্সটিতে ৩টি রো এবং ৩টি কলাম রয়েছে। তাই এটি একটি ৩ x ৩ স্কয়ার ম্যাট্রিক্স। স্কয়ার ম্যাট্রিক্স এ দুটি কর্ণ থাকে। বাম দিক থেকে শুরু হওয়া কর্ণটিকে বলা প্রাইমারি ডায়াগোনাল এবং ডান দিক থেকে শুরু হওয়া কর্ণটিকে বলা সেকেন্ডারি ডায়াগোনাল।

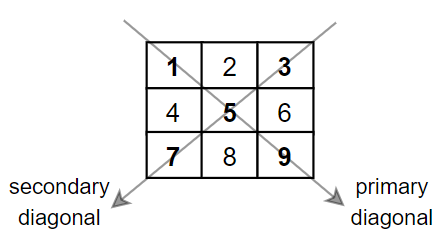
ডায়াগোনাল ম্যাট্রিক্সঃ

ডায়াগোনাল ম্যাট্রিক্স হলো এমন একটি স্কয়ার ম্যাট্রিক্স যার শুধুমাত্র কর্ণ বরাবর ভেলু থাকে বাকি সব ভেলু জিরো থাকে। পাশের স্কয়ার ম্যাট্রিক্সটিতে শুধুমাত্র প্রাইমারি ডায়াগোনাল বরাবর ভেলু রয়েছে বাকি সব ভেলু জিরো, তাই এটি একটি ডায়াগোনাল ম্যাট্রিক্স।

স্কেলার ম্যাট্রিক্সঃ

স্কেলার ম্যাট্রিক্স হলো এমন একটি ডায়াগোনাল ম্যাট্রিক্স যার সবগুলো ভেলুই সেইম। পাশের ম্যাট্রিক্সটিতে শুধুমাত্র প্রাইমারি ডায়াগোনাল বরাবর ভেলু রয়েছে বাকি সব ভেলু জিরো, তাই এটি একটি ডায়াগোনাল ম্যাট্রিক্স। আবার কর্ণ বরাবর থাকা ভেলুগুলো সব সেইম, তাই এটি একটি স্কেলার ম্যাট্রিক্স।

ইউনিট ম্যাট্রিক্সঃ

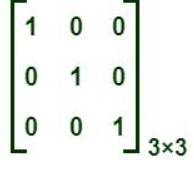
ইউনিট ম্যাট্রিক্স হলো এমন একটি স্কেলার ম্যাট্রিক্স যার সবগুলো ভেলুই ১। পাশের ম্যাট্রিক্সটিতে শুধুমাত্র প্রাইমারি ডায়াগোনাল বরাবর ভেলু রয়েছে বাকি সব ভেলু জিরো, তাই এটি একটি ডায়াগোনাল ম্যাট্রিক্স। আবার কর্ণ বরাবর থাকা ভেলুগুলো সব সেইম, তাই এটি একটি স্কেলার ম্যাট্রিক্স। আবার কর্ণ বরাবর থাকা সবগুলো ভেলুই ১, তাই এটি একটি ইউনিট ম্যাট্রিক্স।

আরো অনেক ধরনের ম্যাট্রিক্স রয়েছে। আমাদের 2D এরে ভালোভাবে বুঝার জন্য এই কয়টি ম্যাট্রিক্স জানলেই চলবে।

---

মডিউল ১৮-৯ + ১৮-১০ঃ রো ম্যাট্রিক্স, কলাম ম্যাট্রিক্স, স্কয়ার ম্যাট্রিক্স, জিরো অথবা নাল ম্যাট্রিক্স

রো ম্যাট্রিক্স কি?

রো ম্যাট্রিক্স হলো একটি বিশেষ ধরনের ম্যাট্রিক্স যার শুধুমাত্র ১টি সারি (row) থাকে এবং ১ বা তার বেশি কলাম (column) থাকতে পারে।

রো ম্যাট্রিক্স (Row Matrix) এর সি প্রোগ্রাম

Code:

#include <stdio.h>
int main()
{
    int r, c;  // r = রো (সারি) সংখ্যা, c = কলাম সংখ্যা

    // ইউজার থেকে ম্যাট্রিক্সের সারি ও কলাম সংখ্যা ইনপুট নেওয়া
    scanf("%d %d", &r, &c);

    // r x c সাইজের 2D অ্যারে (ম্যাট্রিক্স) ডিক্লেয়ার করা
    int a[r][c];

    // নেস্টেড লুপ ব্যবহার করে ম্যাট্রিক্সের প্রতিটি এলিমেন্ট ইনপুট নেওয়া
    for (int i = 0; i < r; i++)      // বাইরের লুপ - সারি (row) এর জন্য
    {
        for (int j = 0; j < c; j++)  // ভিতরের লুপ - কলাম (column) এর জন্য
        {
            scanf("%d", &a[i][j]);   // ম্যাট্রিক্সের [i][j] পজিশনের এলিমেন্ট ইনপুট নেওয়া
        }
    }

    // রো ম্যাট্রিক্স চেক করার শর্ত
    if (r == 1)  // যদি ম্যাট্রিক্সে শুধুমাত্র ১টি সারি থাকে
    {
        printf("Row matrix.");  // তাহলে এটি রো ম্যাট্রিক্স
    }
    else
    {
        printf("Not Row matrix.");  // নতুবা এটি রো ম্যাট্রিক্স নয়
    }

    return 0;  // প্রোগ্রাম সফলভাবে শেষ হয়েছে
}

প্রোগ্রামের আউটপুট উদাহরণ:

ইনপুট:

1 3
1 2 3

আউটপুট:

Row matrix.

ইনপুট:

2 3
1 2 3
4 5 6

আউটপুট:

Not Row matrix.

কলাম ম্যাট্রিক্স কি?

কলাম ম্যাট্রিক্স হলো একটি বিশেষ ধরনের ম্যাট্রিক্স যার শুধুমাত্র ১টি কলাম (column) থাকে এবং ১ বা তার বেশি সারি (row) থাকতে পারে।

কলাম ম্যাট্রিক্স (Column Matrix) এর সি প্রোগ্রাম:

Code:

#include <stdio.h>
int main()
{
    int r, c;  // r = রো (সারি) সংখ্যা, c = কলাম সংখ্যা

    // ইউজার থেকে ম্যাট্রিক্সের সারি ও কলাম সংখ্যা ইনপুট নেওয়া
    scanf("%d %d", &r, &c);

    // r x c সাইজের 2D অ্যারে (ম্যাট্রিক্স) ডিক্লেয়ার করা
    int a[r][c];

    // নেস্টেড লুপ ব্যবহার করে ম্যাট্রিক্সের প্রতিটি এলিমেন্ট ইনপুট নেওয়া
    for (int i = 0; i < r; i++)      // বাইরের লুপ - সারি (row) এর জন্য
    {
        for (int j = 0; j < c; j++)  // ভিতরের লুপ - কলাম (column) এর জন্য
        {
            scanf("%d", &a[i][j]);   // ম্যাট্রিক্সের [i][j] পজিশনের এলিমেন্ট ইনপুট নেওয়া
        }
    }

    // কলাম ম্যাট্রিক্স চেক করার শর্ত
    if (c == 1)  // যদি ম্যাট্রিক্সে শুধুমাত্র ১টি কলাম থাকে
    {
        printf("Column matrix.");  // তাহলে এটি কলাম ম্যাট্রিক্স
    }
    else
    {
        printf("Not Column matrix.");  // নতুবা এটি কলাম ম্যাট্রিক্স নয়
    }

    return 0;  // প্রোগ্রাম সফলভাবে শেষ হয়েছে
}

প্রোগ্রামের আউটপুট উদাহরণ:

ইনপুট:

3 1
1
2
3

আউটপুট:

Column matrix.

ইনপুট:

2 3
1 2 3
4 5 6

আউটপুট:

Not Column matrix.

স্কয়ার ম্যাট্রিক্স কি?

স্কয়ার ম্যাট্রিক্স হলো একটি বিশেষ ধরনের ম্যাট্রিক্স যার সারি এবং কলাম সংখ্যা সমান (r == c)।

স্কয়ার ম্যাট্রিক্স (Square Matrix) এর সি প্রোগ্রাম

Code:

#include <stdio.h>
int main()
{
    int r, c;  // r = রো (সারি) সংখ্যা, c = কলাম সংখ্যা

    // ইউজার থেকে ম্যাট্রিক্সের সারি ও কলাম সংখ্যা ইনপুট নেওয়া
    scanf("%d %d", &r, &c);

    // r x c সাইজের 2D অ্যারে (ম্যাট্রিক্স) ডিক্লেয়ার করা
    int a[r][c];

    // নেস্টেড লুপ ব্যবহার করে ম্যাট্রিক্সের প্রতিটি এলিমেন্ট ইনপুট নেওয়া
    for (int i = 0; i < r; i++)      // বাইরের লুপ - সারি (row) এর জন্য
    {
        for (int j = 0; j < c; j++)  // ভিতরের লুপ - কলাম (column) এর জন্য
        {
            scanf("%d", &a[i][j]);   // ম্যাট্রিক্সের [i][j] পজিশনের এলিমেন্ট ইনপুট নেওয়া
        }
    }

    // স্কয়ার ম্যাট্রিক্স চেক করার শর্ত
    if (r == c)  // যদি ম্যাট্রিক্সের সারি এবং কলাম সংখ্যা সমান হয়
    {
        printf("Square matrix.");  // তাহলে এটি স্কয়ার ম্যাট্রিক্স
    }
    else
    {
        printf("Not Square matrix.");  // নতুবা এটি স্কয়ার ম্যাট্রিক্স নয়
    }

    return 0;  // প্রোগ্রাম সফলভাবে শেষ হয়েছে
}

প্রোগ্রামের আউটপুট উদাহরণ:

ইনপুট:

3 3
1 2 3
4 5 6
7 8 9

আউটপুট:

Square matrix.

ইনপুট:

2 3
1 2 3
4 5 6

আউটপুট:

Not Square matrix.

জিরো বা নাল ম্যাট্রিক্স

এবার আমরা 2D এরের সাহায্যে একটি ম্যাট্রিক্স ইনপুট নিয়ে তা জিরো বা নাল ম্যাট্রিক্স কিনা তা বের করব।

প্রথমে ম্যাট্রিক্সটির রো এবং কলাম ইনপুট নিয়ে সেই রো এবং কলাম দিয়ে একটি 2D এরে ডিক্লেয়ার করে ফেলতে পারি। তারপর ম্যাট্রিক্সটি ইনপুট নেওয়ার পর আমরা একটি সিম্পল লজিক দিয়ে ফেলতে পারি তা হলো আমরা ম্যাট্রিক্স এর মধ্যে জিরো পেলেই তা কাউন্ট করে রাখব। লাস্টে আমরা চেক করে দেখব আমাদের কাউন্ট আমাদের সবগুলো এলিমেন্ট সংখ্যার সাথে মিলছে কিনা। জিরো ম্যাট্রিক্স হলে সবগুলো এলিমেন্টই জিরো হতে হবে। এক্ষেত্রে রো এবং কলাম গুন করলেই আমরা এলিমেন্ট সংখ্যা পেয়ে যাব। তারপর চেক করে দেখব এলিমেন্ট সংখা এবং জিরো কাউন্ট সেইম কিনা। সেইম হলে জিরো ম্যাট্রিক্স আর নাহলে জিরো ম্যাট্রিক্স না।

উদাহরন হিসেবে একটি ৩ x ৫ জিরো ম্যাট্রিক্স এর এলিমেন্ট সংখ্যা হবে ( ৩ * ৫ ) = ১৫ আর তাতে জিরো থাকতে হবে ১৫টি।

Code:

#include <stdio.h>
int main()
{
    int row, col;
    scanf("%d %d", &row, &col); // রো এবং কলাম ইনপুট নেওয়া হচ্ছে।
    int a[row][col];                    // সেই রো এবং কলাম দিয়ে একটি 2D এরে ডিক্লেয়ার করা হচ্ছে।
    int element = row * col;            // রো এবং কলাম গুন করে এলিমেন্ট সংখ্যা বের করা হচ্ছে।
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            scanf("%d", &a[i][j]);      // ম্যাট্রিক্স ইনপুট নেওয়া হচ্ছে।
        }
    }
    int cnt = 0;                        // জিরো কাউন্ট করার জন্য ভেরিয়েবল নিয়ে ০ দিয়ে ইনিশিয়াল করা হয়েছে।
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            if (a[i][j] == 0)           // নেস্টেড লুপ চালিয়ে সম্পূর্ণ ম্যাট্রিক্স এ যেয়ে ০ কাউন্ট করা হচ্ছে।
            {
                cnt++;
            }
        }
    }
    if (element == cnt)                 // চেক করা হচ্ছে এলিমেন্ট সংখ্যা এবং জিরো সংখ্যা সেইম কিনা।
    {
        printf("Zero matrix\n");        // সেইম হলে জিরো ম্যাট্রিক্স।
    }
    else
    {
        printf("Not zero matrix\n");    // আর সেইম না হলে জিরো ম্যাট্রিক্স না।
    }
    return 0;
}

---

মডিউল ১৮-১১ + ১৮-১২ঃ ডায়াগোনাল ম্যাট্রিক্স ইউজিং 2D এরে

এবার আমরা 2D এরের সাহায্যে একটি ম্যাট্রিক্স ইনপুট নিয়ে তা প্রাইমারি ডায়াগোনাল বা সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স কিনা তা বের করব।

প্রাইমারি ডায়াগোনাল ম্যাট্রিক্সঃ

আমরা যদি একটি 2D এরেতে প্রাইমারি ডায়াগোনাল এর ইন্ডেক্সগুলো খেয়াল করি:

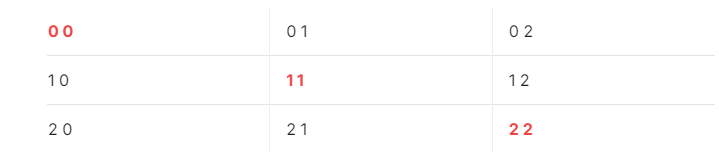
তাহলে দেখতে পাব ইন্ডেক্সে রো এবং কলাম সেইম হচ্ছে। অর্থাৎ আমরা যদি দেখি ইনডেক্সে রো এবং কলাম সেইম তাহলে বুঝতে পারব আমরা এখন প্রাইমারি ডায়াগোনাল এর উপরে আছি।

তাহলে এভাবে আমরা চেক করে ফেলতে পারি একটি ম্যাট্রিক্স প্রাইমারি ডায়াগোনাল কিনা। শুরুতেই আমরা চেক করব ম্যাট্রিক্সটি স্কয়ার কিনা, স্কয়ার না হলে ডায়াগোনাল ম্যাট্রিক্স হবে না। তারপর আমরা পুরো ম্যাট্রিক্স এ যেয়ে যখনি আমরা প্রাইমারি ডায়াগোনাল এর উপরে থাকব না তখনি চেক করে দেখব ওখানে ভেলু জিরো আছে কিনা। যদি জিরো না থাকে তাহলে সেটি প্রাইমারি ডায়াগোনাল ম্যাট্রিক্স হবে না।

Code:

#include <stdio.h>
int main()
{
    int row, col;
    scanf("%d %d", &row, &col);
    int a[row][col];
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            scanf("%d", &a[i][j]);      // ম্যাট্রিক্স ইনপুট নিচ্ছি।
        }
    }
    int flag = 1;                       // একটি ফ্ল্যাগ ভেরিয়েবল নিয়ে শুরুতে ১ রেখে দিচ্ছি। যখনি দেখব প্রাইমারি ডায়াগোনাল ম্যাট্রিক্স না তখনি তাতে ০ রেখে দিব।
    if (row != col)                     // শুরুতে চেক করছি এটি একটি স্কয়ার ম্যাট্রিক্স কিনা।
    {
        flag = 0;                       // স্কয়ার ম্যাট্রিক্স না হলে ডায়াগোনাল ম্যাট্রিক্স হবে না তাই ফ্ল্যাগ এর মধ্যে ০ রেখে দিচ্ছি।
    }
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)   // নেস্টেড লুপ চালিয়ে পুরো ম্যাট্রিক্স এর মধ্যে যাওয়া হচ্ছে।
        {
            if (i == j)                 // যদি রো ইন্ডেক্স এবং কলাম ইন্ডেক্স সেইম হয় তারমানে এখন আমরা প্রাইমারি ডায়াগোনাল এর উপরে আছি।
            {
                continue;               // প্রাইমারি ডায়াগোনালে আমাদের চেক করার কিছু নেই তাই কন্টিনিউ করছি।
            }
            if (a[i][j] != 0)           // যদি প্রাইমারি ডায়াগোনালে না থাকি এবং ম্যাট্রিক্স এর ভেলু ০ না হয়
            {
                flag = 0;               // তাহলে এটি প্রাইমারি ডায়াগোনাল ম্যাট্রিক্স না, তাই ফ্ল্যাগ এর মধ্যে ০ রেখে দিচ্ছি।
            }
        }
    }
    if (flag == 1)                      // সবশেষে চেক করছি ফ্ল্যাগ এর মধ্যে ১ আছে কিনা।
    {
        printf("Primary Diagonal\n");   // ১ থাকলে এটি একটি প্রাইমারি ডায়াগোনাল ম্যাট্রিক্স।
    }
    else
    {
        printf("Not Primary Diagonal\n"); // আর ১ না থাকলে এটি একটি প্রাইমারি ডায়াগোনাল ম্যাট্রিক্স না।
    }
    return 0;
}

সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্সঃ

আমরা যদি একটি 2D এরেতে সেকেন্ডারি ডায়াগোনাল এর ইন্ডেক্সগুলো খেয়াল করি:

তাহলে দেখতে পাব ইন্ডেক্সে রো এবং কলাম এর যোগফল সেইম হচ্ছে আর তা হচ্ছে রো থেকে ১ কম। সেকেন্ডারি ডায়াগোনাল ছাড়া অন্য কোথাও রো এবং কলাম এর যোগফল রো-১ এর সমান হচ্ছে না। অর্থাৎ আমরা যদি দেখি ইনডেক্সে রো এবং কলামের যোগফল রো-১ এর সমান তাহলে বুঝতে পারব আমরা এখন সেকেন্ডারি ডায়াগোনাল এর উপরে আছি।

তাহলে এভাবে আমরা চেক করে ফেলতে পারি একটি ম্যাট্রিক্স সেকেন্ডারি ডায়াগোনাল কিনা। শুরুতেই আমরা চেক করব ম্যাট্রিক্সটি স্কয়ার কিনা, স্কয়ার না হলে ডায়াগোনাল ম্যাট্রিক্স হবে না। তারপর আমরা পুরো ম্যাট্রিক্স এ যেয়ে যখনি আমরা সেকেন্ডারি ডায়াগোনাল এর উপরে থাকব না তখনি চেক করে দেখব ওখানে ভেলু জিরো আছে কিনা। যদি জিরো না থাকে তাহলে সেটি সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স হবে না।

Code:

#include <stdio.h>
int main()
{
    int row, col;
    scanf("%d %d", &row, &col);
    int a[row][col];
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            scanf("%d", &a[i][j]);      // ম্যাট্রিক্স ইনপুট নিচ্ছি।
        }
    }
    int flag = 1;                       // একটি ফ্ল্যাগ ভেরিয়েবল নিয়ে শুরুতে ১ রেখে দিচ্ছি। যখনি দেখব সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স না তখনি তাতে ০ রেখে দিব।
    if (row != col)                     // শুরুতে চেক করছি এটি একটি স্কয়ার ম্যাট্রিক্স কিনা।
    {
        flag = 0;                       // স্কয়ার ম্যাট্রিক্স না হলে ডায়াগোনাল ম্যাট্রিক্স হবে না তাই ফ্ল্যাগ এর মধ্যে ০ রেখে দিচ্ছি।
    }
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)   // নেস্টেড লুপ চালিয়ে পুরো ম্যাট্রিক্স এর মধ্যে যাওয়া হচ্ছে।
        {
            if (i + j == row - 1)       // যদি রো ইন্ডেক্স এবং কলাম ইন্ডেক্স এর যোগফল রো-১ এর সমান হয় তারমানে এখন আমরা সেকেন্ডারি ডায়াগোনাল এর উপরে আছি।
            {
                continue;               // সেকেন্ডারি ডায়াগোনালে আমাদের চেক করার কিছু নেই তাই কন্টিনিউ করছি।
            }
            if (a[i][j] != 0)           // যদি সেকেন্ডারি ডায়াগোনালে না থাকি এবং ম্যাট্রিক্স এর ভেলু ০ না হয়
            {
                flag = 0;               // তাহলে এটি সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স না, তাই ফ্ল্যাগ এর মধ্যে ০ রেখে দিচ্ছি।
            }
        }
    }
    if (flag == 1)                      // সবশেষে চেক করছি ফ্ল্যাগ এর মধ্যে ১ আছে কিনা।
    {
        printf("Secondary Diagonal\n"); // ১ থাকলে এটি একটি সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স।
    }
    else
    {
        printf("Not Secondary Diagonal\n"); // আর ১ না থাকলে এটি একটি সেকেন্ডারি ডায়াগোনাল ম্যাট্রিক্স না।
    }
    return 0;
}